The Batman Spread

The Batman Options Spread is a sophisticated trading structure that is designed to capitalize on specific market conditions.

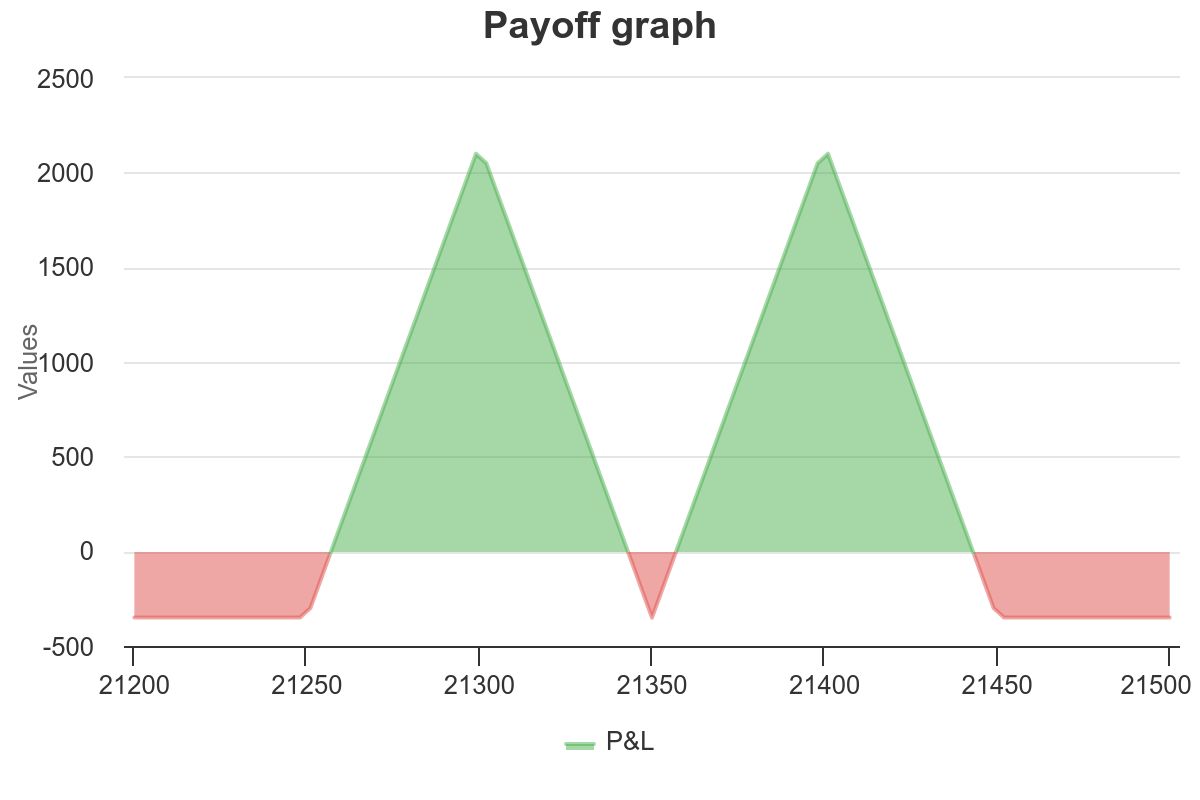
The payoff of this strategy resembles the silhouette of a bat and that’s why it is fondly called Batman Options Strategy!

It got its name in the Unofficed Forum Discussion long ago.

There are many different ways one can end up with this payoff graph.

Neutral Batman Spread

Here we will discuss a spread that is a variation of the Double Long Butterfly Spread which is made of one is a Long Put Butterfly spread and another is a Long Call Butterfly spread.

Combining a Long Put Butterfly Spread with a Long Call Butterfly Spread creates a strategy that is essentially neutral to the direction of the market.

Here’s a detailed breakdown of the strategy:

Setup

• Buy a Straddle – 1x
• Sell a Near Out-of-the-Money (OTM) Strangle – 2x
• Buy an OTM Strangle – 1x

Ideal IV Environment: High

Optimal Conditions After Entry:

Range-Bound with Expected Breakout: The market may have been range-bound but is showing signs of a potential breakout. In such scenarios, the Batman Options Strategy can capitalize on the breakout when it occurs.

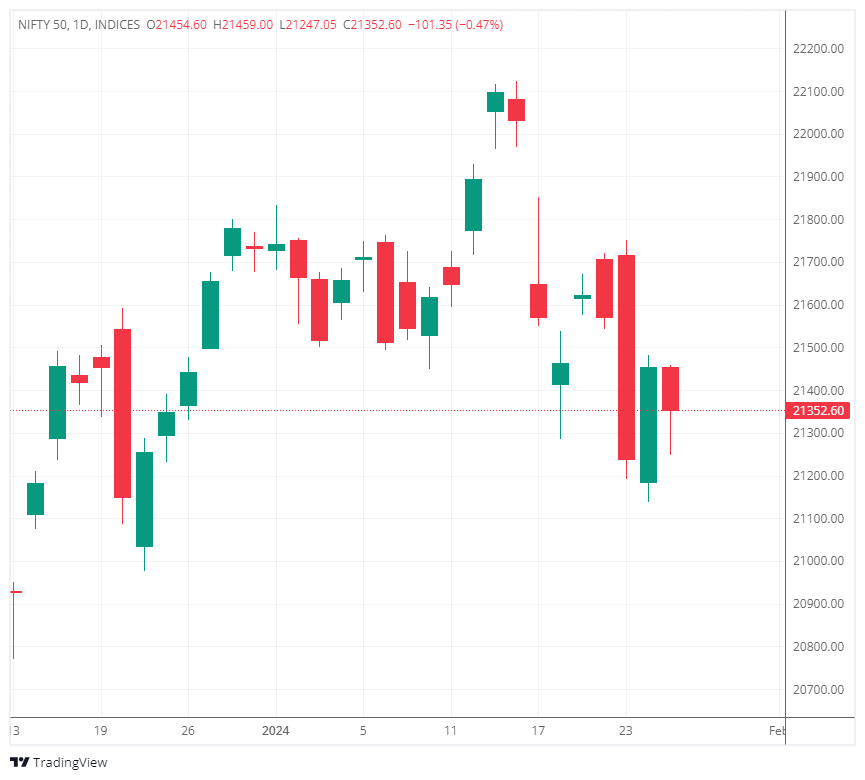
Live Example of Batman Strategy:

To capitalize on the Batman Options Strategy, a trader should ideally:

• Enter the trade when IV is high: This is when the trader expects volatility to spike, leading to higher premiums, especially for the long positions of the straddle and the far OTM strangle.
• Hope for a decrease in IV after trade initiation: This will decrease the value of the short options, potentially leading to a profit when they are bought back or expire worthless.

In the above chart, You can see NIFTY had a gap down followed by sharp bearish days. It means –

1. Due to recent volatility, the IV is high.  
2. It is currently in a range-bound manner (It formed an inside bar last day showing confusion) and a breakout can happen anytime.

It satisfies the best optimal condition!

So, Let’s execute the strategy as seen here –

https://unofficed.com/options-calculator/?save_id=65b58dfb2e098497445618

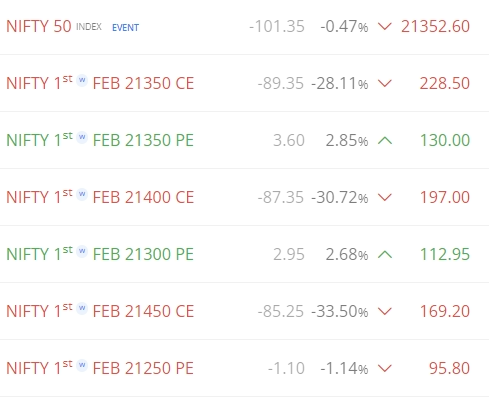
1. Buy Straddle: Buy 50 Nifty Calls and 50 Nifty Puts at the 21350 strike.
2. Sell Near OTM Strangle: Sell 100 Nifty Calls at the 21400 strike and 100 Nifty Puts at the 21300 strike.
3. Buy OTM Strangle: Buy 50 Nifty Calls at the 21450 strike and 50 Nifty Puts at the 21250 strike.

Let’s calculate the premium collected and the maximum risk involved:

Premiums for the Straddle (Buy):

• Call premium: 230
• Put premium: 130
• Total premium paid for straddle: (230 + 130) * 50 = 18,000

Premiums for the Near OTM Strangle (Sell):

• Call premium: 197
• Put premium: 112
• Total premium received for strangle: (197 + 112) * 100 = 30,900

Premiums for the OTM Strangle (Buy):

• Call premium: 169.2
• Put premium: 95.8
• Total premium paid for strangle: (169.2 + 95.8) * 50 = 13,250

Net Premium Received:

• Total premium received for selling strangle – Total premium paid for buying straddle and strangle
• Net premium = 30,900 – (18,000 + 13,250) = -370

Assuming that the net premium is negative, the trader will need the market to move enough to cover the cost of the premiums paid.

The maximum loss here is 370 INR only.

Profit and Loss Diagram

The payoff graph provided with the image indicates two profit peaks with a trough in between.

The ideal IV environment would have the following effects:

At the Peaks: High IV leads to greater premiums collected from the sold near OTM strangle. The strategy aims to maintain these peaks, where the profit potential is maximized.

• Note 1: The peak occurs at the strike where we have sold the Near OTM Strangle.
• Note 2: Although there is a range and it makes a loss if the range is broken, It also makes a loss in the middle where we have bought the ATM Straddle!

At the Trough: If IV decreases after the strategy is in place, it reduces the value of the options sold, which is advantageous since the trader wants these options to expire worthless or be bought back at a lower price.

The ideal market conditions should enable the underlying asset’s price to finish near the peaks or within the trough at expiration for the strategy to be profitable.

Volatility Skew and Batman Options Strategy

In the context of the Batman Options Strategy, volatility skew is a critical element.

The volatility skew refers to the pattern where options with different strike prices but the same expiration date have different levels of implied volatility (IV).

Typically, out-of-the-money (OTM) options have higher IV than at-the-money (ATM) options due to the increased uncertainty and risk of ending up in-the-money as the option moves further from the current price of the underlying asset.

Here’s how the volatility skew plays a role in the Batman Options Strategy:

Selling Near OTM Options:

• The long positions (straddle and far OTM strangle) have a higher vega, meaning they are more sensitive to changes in IV.
• A high IV at entry will inflate the value of these options.

This part of the strategy aims to collect premiums while minimizing the risk associated with large swings in IV.

Buying Far OTM Options:

• The short positions (near OTM strangle) have a lower vega compared to the long positions, so while they benefit from high IV at entry (higher premium collected), they are less sensitive to a drop in IV.
• However, any drop in IV will still reduce their price, which is beneficial when it comes time to close the position.

This aspect of the strategy is designed to protect against large, unexpected moves that could result in significant losses on the short near OTM options.

The strategy aims to balance the premiums received from selling the near OTM options against the cost of buying the far OTM options. In an ideal setup, the premiums from the sold options should be sufficient to cover the cost of the bought options, with excess premium representing potential profit.

The volatility skew is thus both a risk factor and an opportunity within the Batman Options Strategy. It necessitates careful consideration of the relative premiums and IV levels of the options at different strike prices.