Continuous Compounding
In the world of finance, the concept of compounding interest plays a pivotal role in determining the growth of investments and the cost of loans. Interest can be compounded at various intervals, such as monthly, quarterly, or semiannually. However, there exists a mathematical wonder known as continuous compounding, where interest is calculated and added to the principal continuously, at every infinitesimally small instant.
This method leads to a higher effective interest rate, making it a significant concept in the stock market. In this comprehensive exploration, we will delve into the intricacies of continuous compounding, its applications in the stock market, and its implications for investors.
Understanding Continuous Compounding
Continuous compounding is a financial concept that defies traditional periodic interest calculations. Instead of adding interest to the principal at fixed intervals, it considers an infinite number of compounding moments over a specified time period. This results in a continuously growing investment, making it a powerful tool for investors seeking to maximize their returns.
The formula for calculating the total account value with continuous compounding is:
Where:
- T is the total account value
- P is the principal invested
- e is the mathematical constant, approximately equal to 2.7183
- i is the interest rate
- t is the time
Now, let’s illustrate this concept with a practical example. Suppose you invest 10,000 INR at an annual interest rate of 15%. We can calculate the total account value based on different compounding frequencies:
Annual Compounding:
T = 10,000 × (1 + (15% / 1)) × (1 × 1) = 11,500
Semi-Annual Compounding:
T = 10,000 × (1 + (15% / 2)) × (2 × 1) = 11,556.25
Quarterly Compounding:
T = 10,000 × (1 + (15% / 4)) × (4 × 1) = 11,586.50
Monthly Compounding:
T = 10,000 × (1 + (15% / 12)) × (12 × 1) = 11,607.55
Daily Compounding:
T = 10,000 × (1 + (15% / 365)) × (365 × 1) = 11,617.98
In continuous compounding, the number of compounding periods (n) tends towards infinity, reflecting the ever-changing nature of the stock market.
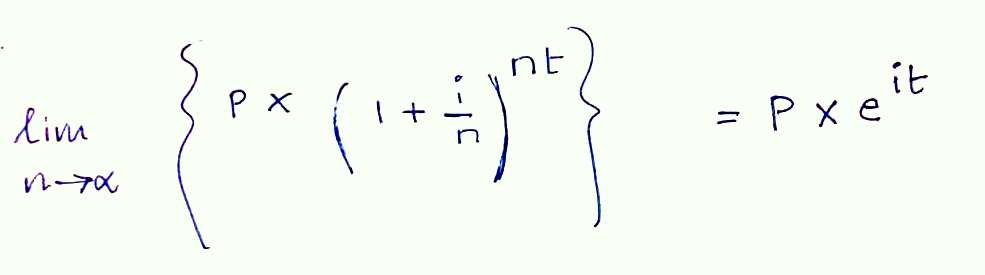
- T=P×ei×t
Continuous Compounding in the Stock Market
As we can see, the choice of compounding frequency can significantly impact the total account value. But how does continuous compounding fit into the chaos of the stock market, where investments and trading activities occur on diverse timescales?
The stock market is a dynamic and unpredictable environment. Unlike traditional investments with fixed compounding intervals, the stock market operates without a structured compounding period. Investors engage in various strategies, including long-term investing, positional trading, and day trading. Moreover, the stock market is prone to both growth and loss, making it a complex ecosystem for wealth creation.
Let’s calculate the total account value for our example of a 10,000 INR investment with 15% annual interest rate using continuous compounding:
T = 10,000 × 2.7183^(15% × 1) ≈ 11,618.34
It’s intriguing to note that many investors claim that in the stock market, compounding effectively occurs daily. When comparing daily compounding with continuous compounding, we find that the difference in total interest earned is minimal:
It’s intriguing to note that many investors claim that in the stock market, compounding effectively occurs daily. When comparing daily compounding with continuous compounding, we find that the difference in total interest earned is minimal:
- Daily Compounding: 11,617.98
- Continuous Compounding: 11,618.34
The difference is a mere 0.36 INR. Even if we increase the initial investment to a substantial 1 crore INR, the difference remains relatively small at 358 INR.
Understanding Logarithmic Return
- I is the logarithmic return, also referred to as continuously compounded return or the force of interest.
- P represents the principal amount invested.
- T denotes the total account value.
- i is the logarithmic rate of return over a specific time period t.
Assuming reinvestment, we can express the relationship between logarithmic return (I) and logarithmic rate of return (i) for a duration of t as:
I = i × t
Logarithmic return essentially measures the return achieved over a period t. When t is equal to 1, it corresponds to the annualized logarithmic rate of return.
Substituting the value of I, we get: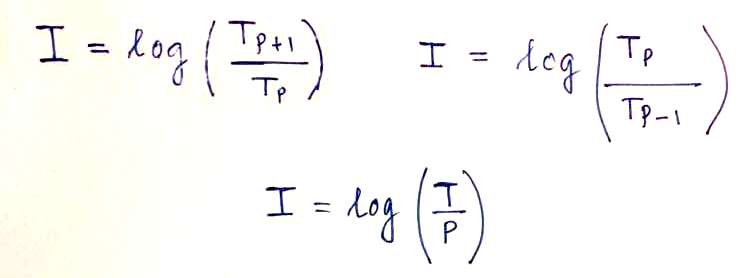
This concept aligns with our previous definition but in a reversed manner.
In the realm of finance, logarithmic return, denoted as “I,” plays a vital role in assessing investment performance. It is also known as continuously compounded return or the force of interest. Logarithmic return reflects the rate at which an investment grows over time, assuming that earnings are reinvested.
To establish the relationship between logarithmic return (I) and the logarithmic rate of return (i) over a specific time period (t), we use the formula:
I = i × t
In simpler terms, logarithmic return represents the return on an investment over a period of time (t). When I = 1 and t = 1, it is referred to as the annualized logarithmic rate of return.
In the context of stock market returns, the primary focus is often on the annualized logarithmic rate of return. This aligns with our previous definition of continuous compounding, where i represents the interest rate of continuously compounded return and is synonymous with the logarithmic rate of return.
Calculating Logarithmic Returns
Let’s apply the concept of logarithmic return to a practical scenario. Suppose you have made an investment with the following details:
- Principal (P): 1,193,403.12 INR
- Profit (P’ = P + 1 – P): 163,957.99 INR
- Time (t): 40 days
To calculate the simple return, we can use the formula:
- Simple Return (%) = (Profit / Principal) × 100
- Simple Return (%) = (163,957.99 / 1,193,403.12) × 100 ≈ 13.7386%
Now, let’s calculate the logarithmic return for the same data. In this case, “t” represents the fraction of a year (40 days out of 365 days). The formula for logarithmic return is:
Logarithmic Return = log(P’ / P)
However, as “t” is relatively small, we can approximate log(1) as 0, and log(t) as 0 as well. Therefore, the rate of return in 40 days can be simplified to:
Logarithmic Return in 40 days = log(P’ / P)
Calculating this:
Logarithmic Return in 40 days = log(1,193,403.12 + 163,957.99 / 1,193,403.12)
The logarithmic return in this case is approximately 12.8733%.
The concept of continuous compounding introduces a fascinating dimension to financial calculations, offering a glimpse into the world of exponential growth. In practical terms, it allows investors to envision the potential of their investments when interest is applied continuously.
In the stock market, where chaos reigns and investments occur on various timescales, continuous compounding serves as a theoretical framework that approximates the dynamics of wealth accumulation. While investors may not experience true continuous compounding, the concept provides valuable insights into the potential growth of investments.
Logarithmic return, on the other hand, offers a precise way to measure the rate of investment growth over time, accounting for reinvestment. It is a valuable tool for comparing different investment strategies and assessing the performance of investment portfolios.
In summary, continuous compounding and logarithmic return are essential concepts in finance that shed light on the power of compounding and the intricacies of investment growth. While the stock market may be a realm of chaos, these mathematical principles provide a foundation for understanding and optimizing financial decisions.

