Next Lesson

Options Premium Calculator using Black Scholes Model: Google Sheet

Option Greeks Options Premium Calculator using Black Scholes Model: Google Sheet

Inputs in Black-Scholes Option Pricing Model Formula

S0 = underlying price
X = strike price
σ = volatility
r = continuously compounded risk-free interest rate
q = continuously compounded dividend yield
t = time to expiration

For,

σ = Volatility = India VIX has been taken.
r = 10% (As per NSE Website, it is fixed.)
q = 0.00% (Assumed No Dividend)

Note: In many resources, you can find different symbols for some of these parameters.

For example,

The strike price is often denoted K (here it is X).
Underlying price is often denoted S (without the zero)
Time to expiration is often denoted T – t (difference between expiration and now).

In the original Black and Scholes paper (The Pricing of Options and Corporate Liabilities, 1973) the parameters were denoted x (underlying price), c (strike price), v (volatility), r (interest rate), and t* – t (time to expiration).

The dividend yield was only added by Merton in Theory of Rational Option Pricing, 1973.

Call and Put Option Price Formulas

Call option C and put option P prices are calculated using the following formulas:

where N(x) is the standard normal cumulative distribution function.

The formulas for d1 and d2 are:

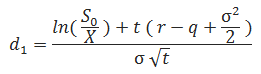
Original Black-Scholes vs. Merton’s Formulas

In the original Black-Scholes model, which doesn’t account for dividends, the equations are the same as above except:

There is just S0 in place of S0 e-qt
There is no q in the formula for d1

Therefore, if the dividend yield is zero, then e-qt = 1 and the models are identical.

Black-Scholes Formulas for Option Greeks

Delta

Theta

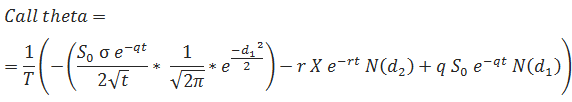
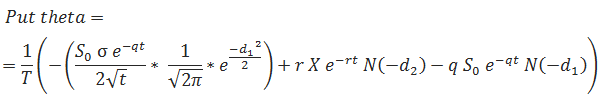
… where T is the number of days per year (calendar or trading days, depending on what you are using).

Gamma

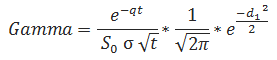
Vega

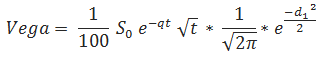
Rho

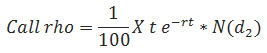
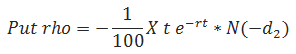
Excel/Google Sheet Formulas for Calculation of Black Scholes Model

Underlying Price: B1
ATM Strike Price: B2
Today’s Date: B3
Expiry Date: B4
Historical Volatility: B5
Risk-Free Rate: B6
Dividend Yield: B7
DTE (Years): B8

d1, d2 Calculation

d1 = (LN(B1/B2)+(B6-B7+0.5*B5^2)*B8)/(B5*SQRT(B8))
Nd1 = EXP(-(B10^2)/2)/SQRT(2*PI())
d2 = B10-B5*SQRT(B8)
Nd2 = NORMSDIST(B12)

Calculation Of Greeks

If You see the above formulas, these are derived directly from those formulas –

Call Theta = (-((B1*B5*EXP(-B7*B8))/(2*SQRT(B8))*(1/(SQRT(2*PI())))*EXP(-(B10*B10)/2))-(B6*B2*EXP(-B6*B8)*NORMSDIST(B12))+(B7*EXP(-B7*B8)*B1*NORMSDIST(B10)))/365
Put Theta = (-((B1*B5*EXP(-B7*B8))/(2*SQRT(B8))*(1/(SQRT(2*PI())))*EXP(-(B10*B10)/2))+(B6*B2*EXP(-B6*B8)*NORMSDIST(-B12))-(B7*EXP(-B7*B8)*B1*NORMSDIST(-B10)))/365
Call Premium = EXP(-B7*B8)*B1*NORMSDIST(B10)-B2*EXP(-B6*B8)*NORMSDIST(B10-B5*SQRT(B8))
Put Premium = B2*EXP(-B6*B8)*NORMSDIST(-B12)-EXP(-B7*B8)*B1*NORMSDIST(-B10)
Call Delta = EXP(-B7*B8)*NORMSDIST(B10)
Put Delta = EXP(-B7*B8)*(NORMSDIST(B10)-1)
Gamma = (EXP(-B6*B8)/(B1*B5*SQRT(B8)))*(1/(SQRT(2*PI())))*EXP(-(B10*B10)/2)
Vega = (EXP(-B6*B8)/(B1*B5*SQRT(B8)))*(1/(SQRT(2*PI())))*EXP(-(B10*B10)/2)
Call Rho = (1/100)*B2*B8*EXP(-B6*B8)*NORMSDIST(B12)
Put Rho = (-1/100)*B2*B8*EXP(-B6*B8)*NORMSDIST(-B12)

Previous Lesson

Back to Course

Next Lesson

Inputs in Black-Scholes Option Pricing Model Formula

Call and Put Option Price Formulas

Original Black-Scholes vs. Merton’s Formulas