Standard Deviation & Options
“It’s more like managing a rollercoaster ride – you never know when you’ll hit a sudden drop or loop-de-loop.”
What is Standard Deviation?
Standard deviation is a statistical measure of the amount of variation in a set of data. In options trading, standard deviation is used to calculate the expected range of price movement for an underlying asset. This range is known as the standard deviation range and is used to predict the potential movement of an option’s price.
Traders use standard deviation to assess the potential risk and reward of an options trade. A higher standard deviation indicates a wider range of possible price movement and therefore greater risk. Conversely, a lower standard deviation suggests a narrower range of price movement and a lower risk.
Implied volatility (IV) is a metric that reflects the expected future volatility of the underlying asset, as implied by the option’s price. Options traders use implied volatility to determine whether an option is overpriced or underpriced. The higher the implied volatility, the higher the option premium and vice versa.
How to Find Standard Deviation of an Asset?
Standard deviation and implied volatility are closely related because the former is used to calculate the latter. Once the implied volatility is known, the standard deviation of the underlying asset’s price movements can be calculated using the following formula:
| Standard Deviation = Implied Volatility x Square Root of Time |
If there are 4 days till the expiration of options, Square Root of Time is calculated as sqrt(4/365). In Option Pricing models, it is normally assumed that Options Contracts are introduced 365 days prior to the expiration date. The implied volatility of a stock is synonymous with a one standard deviation range in that stock if there are 365 days to expiry because in that case, Standard Deviation
= Implied Volatility x Square Root of Time
= Implied Volatility x sqrt(365/365)
= Implied Volatility
Let’s assume,
- the last traded price of BankNIFTY is 41350.4.
- 41300PE is trading at 160.15.
- IV of 41300PE is 14.8.
- There are 4 days to expiry.
So, here,
Standard Deviation (σ)
= IV/100 * Sqrt(t)
= 14.8/100 * Sqrt(4/365)
= 0.1578
What Does Standard Deviation Measure?
In options trading, standard deviation (SD) is a statistical measure that represents the amount of variability or dispersion of prices around the average price of an asset.
- A 1 standard deviation (1SD) move implies that there is a 68% chance that the price of the option will be within a range of +/- 1 standard deviation from its current trading price.
- A 2 standard deviation (2SD) move implies that there is a 95% chance that the price of the option will be within a range of +/- 2 standard deviations from its current trading price.
- A 3 standard deviation (3SD) move implies that there is a 99.7% chance that the price of the option will be within a range of +/- 3 standard deviations from its current trading price.
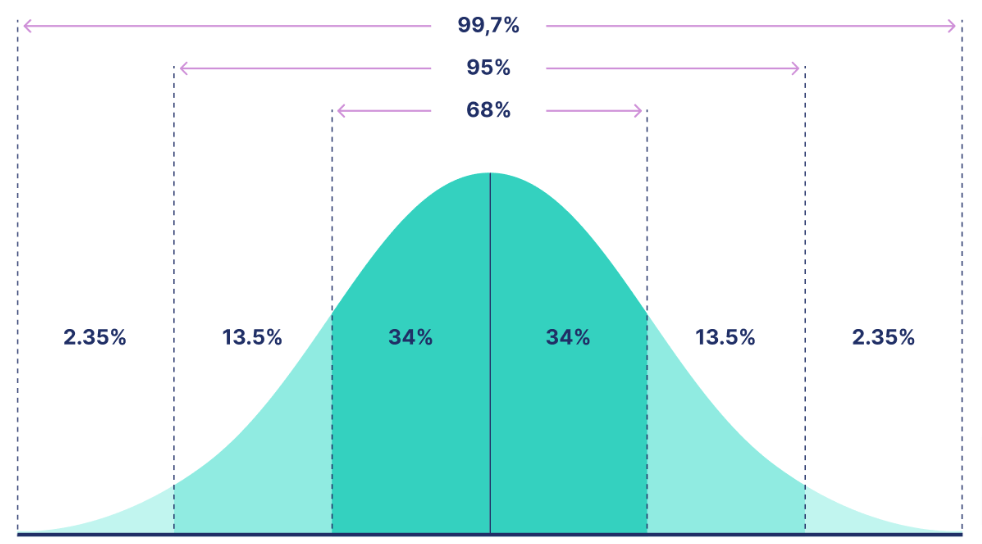
These standard deviation moves are based on a normal distribution and are used by traders to gauge the potential range of price movements for the option.
Normal Distribution In Stock Market
Stock market prices are influenced by a large number of factors, such as economic data, company earnings reports, and geopolitical events. These factors can create a complex and unpredictable environment, making it difficult to predict future prices with certainty.
Normal distribution is a statistical pattern that occurs naturally in many real-world situations, including those with multiple variables or factors. This makes it a useful tool for understanding the probabilities of different outcomes in the stock market.
- The Central Limit Theorem, a fundamental principle of statistics, suggests that the sum of many random variables tends to follow a normal distribution.
- In the context of the stock market, this means that the prices of many individual stocks can be averaged together to form a more stable and predictable overall pattern.
- Empirical studies of stock market data have also shown that stock prices often exhibit a bell-shaped pattern that is consistent with a normal distribution.
- However, it’s important to note that this pattern is not always exact or predictable, and market conditions can shift rapidly and unexpectedly.
Example on How to Calculate and Understand 1SD, 2SD, 3SD
Options traders use these SD values to calculate the probability of an asset’s price reaching a certain level, and to determine the appropriate options strategy to use based on their risk tolerance and market outlook.
So, BankNIFTY 41300PE is trading at 160.15. The standard deviation of this strike is 0.1578. What does it mean?
The standard deviation of the BankNIFTY 41300PE strike being 0.1578 means that the market is expecting the price of this option to fluctuate within a certain range around its current trading price of 160.15.
Assuming a normal distribution, the range of likely price movements for this option can be calculated using the standard deviation.
160.15* 0.1578 = 25.27167 ~ 25.30
- A 1 standard deviation (1SD) move would imply that there is a 68% chance that the price of the option will be between 134.85 (160.15 – 25.30) and 185.45 (160.15 + 25.30) before its expiry.
- A 2 standard deviation(2SD) move would imply that there is a 95% chance that the price of the option will be between 109.55 (160.15 – 25.30*2) and 210.75 (160.15 + 25.30*2) before its expiry.
- A 3 standard deviation (3SD) move would imply that there is a 99.7% chance that the price of the option will be between 84.25 (160.15 – 25.30*3) and 236.05 (160.15 + 25.30*3) before its expiry.
Traders can use this information to make informed decisions about whether to buy or sell this option, based on their risk tolerance and market outlook.
Calculation on Standard Deviation and Probability of Profit
Consider the following query: if the implied volatility (IV) of an option is 12.27%, and the option has an expiration date three days from the present, what must be the delta of an out-of-the-money (OTM) option strike to capture a range of one standard deviation?
Note, the risk-free interest rate is 10%, and the dividend yield is 0% and the price of BankNIFTY stands at 41350.4. Let’s solve this problem:
To calculate the delta of an option that captures a 1 standard deviation range, we first need to determine the expected move of the underlying asset over the 3-day period.
We can do this using the Black-Scholes formula:
- d1 = [ln(S/K) + (r + 0.5σ^2)t] / (σsqrt(t))
- d2 = d1 – σ*sqrt(t)
where:
- S = the current price of the underlying asset
- K = the strike price of the option
- r = the risk-free interest rate
- σ = the implied volatility of the underlying asset
- t = time to expiration (in years)
Using the given information, we can calculate d1 and d2 as follows:
- S = 41350.4
- K = 42000
- r = 0.1
- σ = 0.148
- t = 3/365 = 0.0082
- d1 = [ln(41350.4/42000) + (0.1 + 0.50.1227^2)0.0082] / (0.1227sqrt(0.0082)) = -0.450
- d2 = -0.450 – 0.1227sqrt(0.0082) = -0.471
Next, we need to calculate the expected move of the underlying asset over the 3-day period using the standard deviation formula:
σs = σsqrt(t) = 0.1227sqrt(0.0082) = 0.032
Finally, we can use the delta formula to determine the strike price that captures a 1 standard deviation range:
Δ = N(d1) = 0.326 (from standard normal distribution table)
where N(d1) is the probability that the option will expire in-the-money.
Since we want to capture a 1 standard deviation range, we need to find the strike price that corresponds to a probability of 0.320. This can be done using the inverse of the standard normal distribution:
K
= Sexp[(r – σ^2/2)t + σsinv(N(d1))]
= 41350.4exp[(0.1 – 0.1227^2/2)0.0082 + 0.032inv(N(0.326))]
= 41705.11
Therefore, the delta of an OTM option strike that captures a 1 standard deviation range is approximately 0.320, and the strike price would be Rs. 41,705.11. So, as per this case, Strikes with a probability of 32% ITM / 68% OTM capture a 1 standard deviation range for an OTM option.
Note, We are utilizing a scale of -100 to 100 instead of the more traditional -1 to 1 for delta calculations. Based on this approach, the delta for the given scenario is determined to be 32.
And, the strike price for BankNIFTY would be 41700, as its strike prices of BankNIFTY are presently established in multiples of 100.


Thanks for explaining complicated stuff is simple ways with examples.
The answer is 114114 and 8263. Am I correct
strike price – 16% is the lower range and strikeprice-68% is the OTM range
strike price – 16% is the lower range and strikeprice-68% is the OTM range
I think I m wrong. Tried with the BN Current strike. My formula is not making sense