Implied Volatility

Implied Volatility is an estimate of expected movement in a particular stock or security or asset. It basically tells what the market is “implying” about the volatility.

It is derived from the price of an option in the market. 

The price of the options contract has to be put in the Black-Scholes formulal^[1] and the volatility component gets reverse calculated.

The implied volatility is high when the expected volatility/movement or uncertainty is higher and vice versa.
This expected volatility may be higher due to a variety of reasons like corporate announcements,

 macroeconomic announcements, financial result updates, etc. Due to these, the markets may expect a knee jerk reaction in the prices of the underlying asset which shall result in heightened activity and high volatility in prices i.e. a higher IV or implied volatility.

Note:

• Implied Volatility is a property of options.
• Options have expiration price. So, the Implied Volatility of a deep OTM option will be dynamically lower compared to an ATM option.
• Demand for Put and Call strikes will be different arising asymmetry or so-called skewness to the IV of those aforesaid options.
• Implied volatilities are computed using the Black-Scholes option pricing model.

Generally, for sake of discussion and decision making, the IV of the ATM strike prices are summed and averaged. In some places, one ATM and two subsequent near ATM strike price’s IVs are taken and averaged.

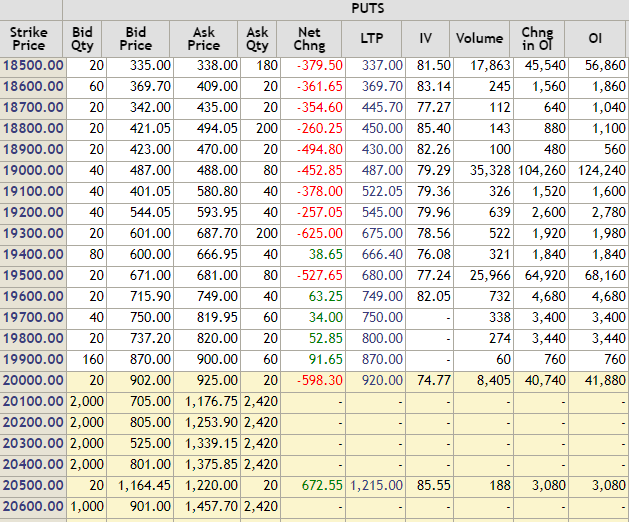
BankNIFTY’s last traded price is 19913.60. The above price is from an option chain^[2] provided by the National Stock Exchange(NSE).

In some cases, We can see blank fields in IV due to the illiquidity of the said contracts.

^[1]Black-Scholes is one of the most popular options pricing models. However, the choice of pricing models varies on traders.

^[2]An option chain, also known as an options matrix, is a listing of all available option contracts, both puts, and calls, for given security within a given maturity period.