Gamma
Gamma tells how delta will change when the underlying asset moves.
Like, A gamma of 0.0032 means We will gain ₹0.0032 delta for every ₹ 1 the underlying asset goes up by. It is a second order derivative of Delta.
Gamma is supposed to move opposite of Theta.
- Gamma is always positive when you buy an option.
- Theta is always negative when you buy an option.
And vice versa.
Gamma Scalping
But there are cases where Gamma and Theta both decrease. These events are highly rare and extremely profitable if captured properly.
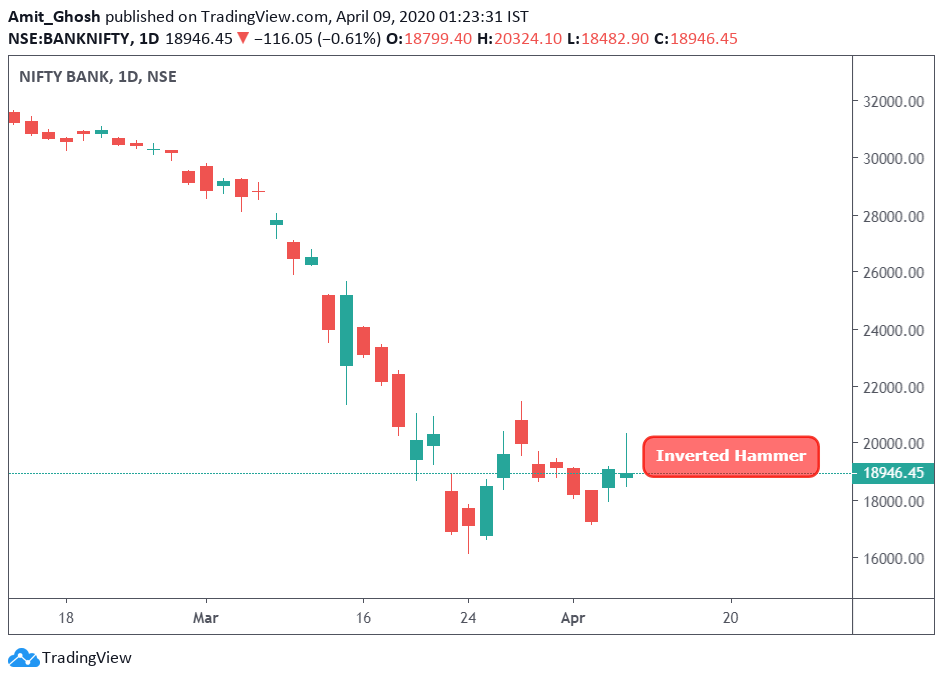
These types of events will create extreme long wicks or long tails. Like, We can see an Inverted Hammer has been created showing extreme rejection from shorters in Intraday.
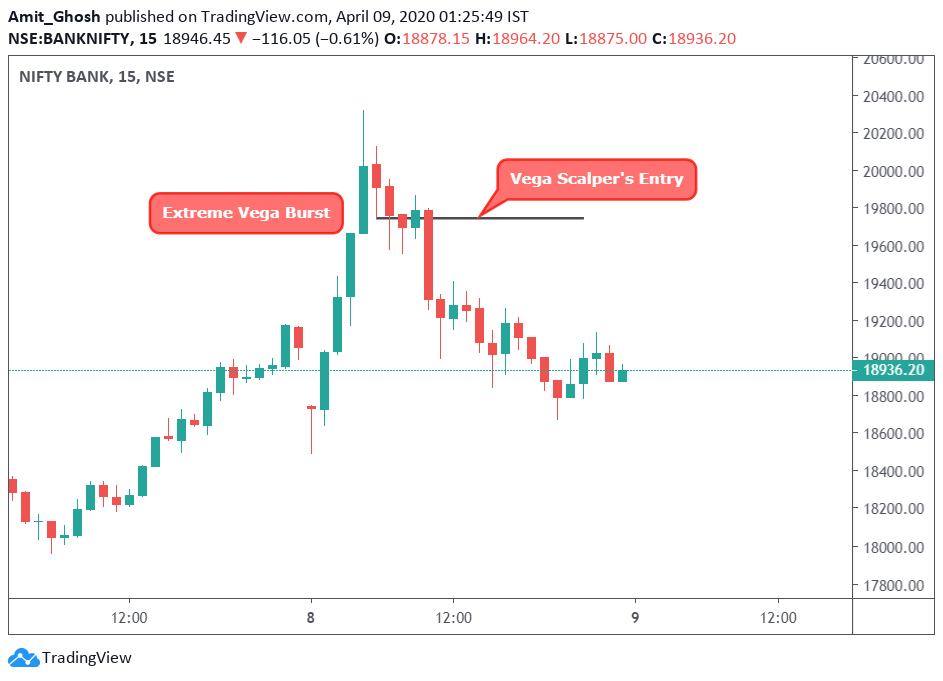
The option’s strike price selection should be based on technicals. Although, that will hence vary person to person as there will be different perception over different time frames.

Notes:
- Theta is a “greek” that represents time decay.
All other things equal, the longer the time elapsed before the maturity date, the less the value of the option. That is, theta is negative over time. - Gamma refers to the “second derivative” of the price of the underlying asset. (The option captures the “delta,” or the first derivative).
As it is a second derivative, gamma is positive when the price of the underlying asset moves towards the strike price of the option, and negative when it moves away. So depending on the price movements, gamma could be either positive or negative, while theta is negative, and the two could thus be positively or negatively correlated.
We already know that maximum Theta erosion happens on the ATM strike price. Now, We can see the effect of Gamma erosion is highest in the ATM strike price again.
Expiration Risk
The most important factor about Gamma is expiration risk. If there is sudden movement of the spot when the expiry is near, then the effect could be devastating for the naked options short holder.
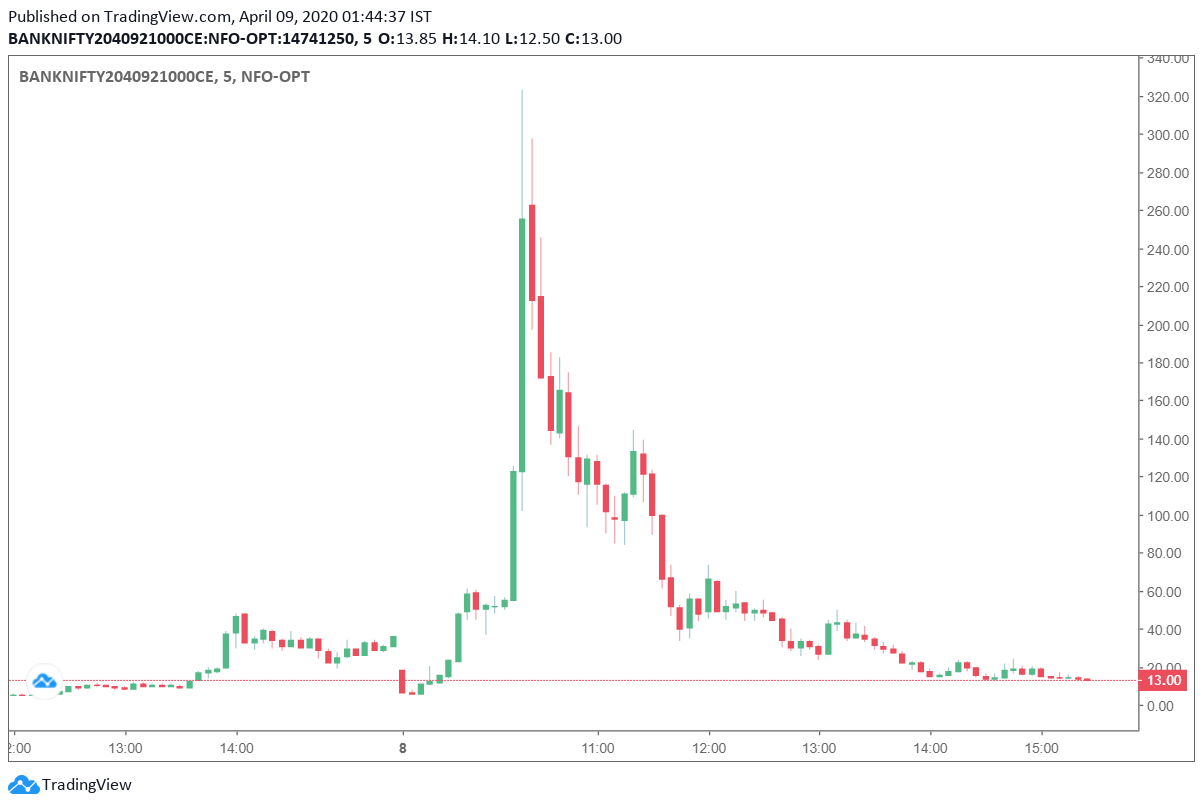
Here is a graph of 9th Apr 21000CE which shows the effect of gamma based on the huge movement as shared in the previous image.
In the image, One can also notice the rapid erosion of premium as the very effect of Gamma starts fading.
It is hard to explain Expiration Risk in a layman way without the help of math but here is a quick summarized version –
- The probability of very deep OTM options going ITM at the end of the expiry is very low. So, the delta’s too small. Hence, the delta will become very high if it becomes ITM.
- So, the rate of change of delta i.e. the gamma will be highly aggressive in this case. The more improbable scenario happens, the more aggression!
Gamma Vs Vega
In volatility spreads,
- Delta is supposed to be neutral.
- Theta is supposed to be moving opposite of Gamma
So, Let’s compare the effect of Gamma and Vega only with respect to the market conditions that will benefit the net positions.
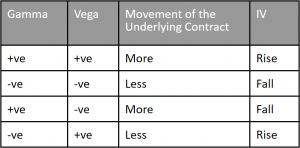
This is the most important table that is needed for the construction and rebalance of volatility spreads.
Effect of Interest Rates
What is Interest Rate in Options Trading?
People often make the mistake of assuming that the interest rate you get from the bank while putting your money is the same interest rate being discussed in Options Trading!
The “interest rate” referred in relation to Options Trading is known as “Risk-Free Interest Rate”. Now, what do you mean by the Risk-Free Interest rate? The Risk-Free Interest Rate is the interest an investor would expect from an absolutely risk-free investment over a given period of time.
Since this interest rate can be obtained with no risk, it is implied that any additional risk taken by an investor should be rewarded with an interest rate higher than the risk-free rate.[1]
Most of the world uses the London Interbank Offered Rate (LIBOR) which is sort of a benchmark interest rate for major global banks. If not LIBOR, Mostly the overnight interbank offered rate of that country is chosen. In India, We use Mumbai Interbank Offer Rate (MIBOR).
You can see live MIBOR rates at https://fbil.org.in/. It’s 4.61% for 3rd April 2020.
Now, By investing in another financial instrument such as Options or buying a stock, the trader is foregoing the risk-free interest they can get on their money. So, option pricing models involve risk-free interest rates!
The annualized continuously compounded rate on MIBOR is then taken into consideration in the Black Scholes Model for the calculation of theoretical options price as the options greek “Rho”.

Effect of Interest Rates on Call Options
Premium of Call options rises when the interest rate rises and vice versa.
Anyways this is obvious because of the Interest Rate Component (Rho) changes in the Black Scholes Options Pricing model. But what can be real life justification for this effect?
Risk Free Interest rate is the opportunity cost for the trader who invests in other financial instruments such as stocks or options. When interest rates are high, the opportunity cost of buying stocks becomes higher. This is what makes buying call options more attractive than buying stocks as we pay a fraction of the cost of the money it takes to buy the actual stocks. The rest of the money is assumed better utilized with risk free returns! Anyways, it theoretically justifies for slightly higher premiums of call options assuming other factors unchanged.
Also, There is the quote: ” As interest rates in the economy increase, the expected return required by investors from the stock tends to increase. In addition, the present value of any future cash flow received by the holder of the option decreases”. So, We are supposed to pay a higher premium for the future obligation of ownership of the stock.
Effect of Interest Rates on Put Options
Premium of Put options falls when the interest rate rises and vice versa. We can use the same arguments used above in case of call options to build up rational reasoning over this comment.
Effect of Interest Rates on Realistic Trading
Interest rate only affects the extrinsic value of an option and not the intrinsic value. So, OTM options having a high extrinsic amount get more affected as well as options with a far expiration cycle get more affected because of the same reason.
But, actually, interest rates rise so slowly that its effects are overshadowed by the price fluctuations caused by other options greek. Interest rate change is a high volatility event which triggers implied volatility and hence, vega! That affects extrinsic value significantly more than interest rates does.
Effect of Dividends
What is Dividend?
When a company makes profit and wants to reward the shareholders for investing in the company, the board of the directors issue payoff per share which is known as Dividend.
Dividend reduces the cash holdings and hence, the total book value of the company. So, An increase in dividends lowers the forward price of the stock and vice versa. The stock price is expected to drop by the amount of the dividend on the ex-dividend date. (Typically, the investor who buys the stocks on its ex-dividend date or later will not be eligible to receive dividends!)
Effects of Dividends on Stock Options
Many options traders are ignorant about the effects of dividends on stock options. In India, We trade European options. Black-Scholes model was designed to evaluate European options only which don’t permit early exercise. So it does not even take dividends into consideration in the calculation of theoretical options premium.
Dividends, however, have the opposite effect on stock options as changes in interest rates.
Effects of Dividends on Put Options
If a stock is expected to drop by a certain amount, that drop would already have been priced into the extrinsic value of its put options way beforehand.
Let’s have a slightly different analogy. If you are short a dividend paying stock, you would be expected to pay back the dividends declared while no such payback is needed if you own its put options instead. This makes owning put options on dividend paying stocks more desirable than shorting the stocks itself.
So, if seen in the reverse way, sellers of put options in dividend paying stocks are assumed to give the dividends.
So, Dividend means higher put premiums.
Effects of Dividends on Call Options
ll the previously discussed analogies can be justified for Call options too.
In short, sellers of call options on dividend paying stocks are assumed to receive the dividends and hence the call options can get discounted by as much as the dividend amount.
So, Dividend means lower call premiums.
Effect of Dividends on Calendar Spreads
- If all the options have the same expiry cycle, the effect of dividend eases out as it will have almost equal effect on all the options. So, the change in the value of the spread will be negligible.
- But, We are having a calendar spread here! If atleast one dividend payment is expected between the expiration cycles, the dividend will cause a call calendar spread to narrow (like premiums of call options get contracted) and will cause a put calendar spread to expand.
A notable fact is – If the stocks pay no dividend, then the value of a call calendar spread should always have more value than 0. It will be at least the worth of cost of carry.
Although there are no greeks associated with dividend risk, we can safely say a call option/spread/calendar spread has negative dividend risk and vice versa.
[1]The risk in government bonds doesn’t come from default since the government can print as much as it likes. But the risk comes from the devaluation of the currency due to inflation (caused by said money printing). Refer to Venezuela, Zimbabwe

