Probability Distribution

A probability distribution is a statistical function that describes all the possible values and likelihoods that a random variable can take within a given range.

There are many different types of probability distributions. One of them is the normal distribution. A probability distribution has a number of factors which is used to describe it – mean, standard deviation, skewness, kurtosis.

We are already aware of mean and standard deviation. But let’s get inside of kurtosis and skewness.

Dispersion

Standard deviation is a measure of the dispersion of a set of data from its mean. If the data points are further from the mean, there is the higher deviation from the data set.
Dispersion is a statistical term describing the size of the range of values expected for a particular variable.
Like, beta is a familiar risk measurement which measures the dispersion of a security’s returns relative to a particular benchmark or market index. You can see how it is calculated in more details here.

Normal Distribution

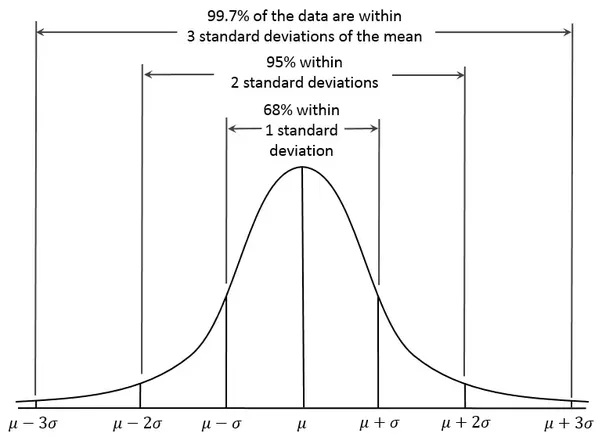
The standard normal distribution or normal distribution is symmetrical data distribution where most of the results lie near the mean.

A standard normal distribution is divided symmetrically using mean of the distribution. ( interpret it as the average of the data set)

Where:

Mu is mean of the distribution
Sigma is the standard deviation

If you consider settings of Bollinger Bands as following –

Period – 20
Standard Deviations – 2
Moving Average Type – Simple

Then it means if we take last 20 price points and plot a line with their average; then it is the median Bollinger.

Here is how it is calculated if you abide by the settings of our 2 SD Bollinger –

Middle Band = 20-day exponential moving average (EMA)
Upper Band = 20-day EMA + (20-day standard deviation of price x 2)
Lower Band = 20-day EMA – (20-day standard deviation of price x 2)

Now if you closely look at the formulas, we can say that 95% prices of a scrip from stock market stay within Bollinger bands of 2 standard deviations.

And, 68% prices of a scrip from stock market stays within Bollinger bands of 1 standard deviation.

Isn’t that amazing?

But we are assuming here that stock market prices follow a standard normal distribution, do they?

Q: Is our assumption that stock market prices follow a standard normal distribution accurate?

A: Let’s illustrate this with a practical example using the 1 Standard Deviation (SD) Bollinger band. These bands, which include upper and lower limits, adjust as the mean changes. According to theory, prices should fall within these limits about 68% of the time.

Q: Can you explain why the Bollinger Bands might not always conform to the 68% and 95% expectations based on a normal distribution?

A: You’re absolutely right. While theory suggests that roughly 68% of data should stay within one standard deviation, and about 95% within two standard deviations, Bollinger Bands work best in stable, range-bound markets. In trending markets, their performance can be less reliable. When we examine historical price charts, such as those for indices like Nifty, we often find that the numbers for 1SD and 2SD are closer to 65% and 90%, respectively.

Q: How does Bollinger Band Riding Strategy (BRS) operate in a trending market?

A: BRS primarily thrives in a ranged market, focusing on the 1 SD to 2 SD range. It signals that a stock has shifted from one range to another. How you trade it and whether you continue to ride it if it crosses 2 SD depends on your exit strategy.

Let’s take an example: Infibeam rises from 1000 to 1010 in a single day. On a linear scale, it appears as a 10-point change, but on a logarithmic price scale, it’s represented as a percentage (or fraction), specifically a 1% change. Now, if Infibeam rises from 1010 to 1020 on another day, it’s still a 10-point move on the linear scale, but on the logarithmic scale, it’s approximately a 0.99% change. The logarithmic scale is crucial because it factors in relative changes, unlike the linear scale.

Q: So, can we conclude that the BRS strategy lacks mathematical backing and relies solely on trader intuition and experience?

A: That’s not accurate. BRS is firmly rooted in mathematical principles. When a stock moves beyond 1 SD, it essentially establishes a new trading range, and the probability of it following the same trend is notably high. This strategy is not just based on intuition or experience; it’s supported by mathematical foundations.

Mean, Median, Mode

The mean is the average of all numbers.

The statistical median is the middle number in a sequence of numbers. If there is an even set of numbers, average the two middle numbers.

The mode is the number that occurs most often within a set of numbers. Mode helps identify the most common or frequent occurrence of a characteristic. It is possible to have two modes (bimodal), three modes (trimodal) or more modes within larger sets of numbers.

Consider the following series as an example: 1, 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 7, 7, 8. This series is described as trimodal because it exhibits three modes, which are 2, 3, and 5. In contrast, a series like 1, 2, 2, 3, 4, 4 is termed bimodal since it has two modes, specifically 2 and 4.