Building a Python Function for Gann Square of 9 Calculator
Importing Necessary Libraries
To begin, we import the math library, which will be used for mathematical calculations throughout the script.
import math
Defining the Main Function
Next, we define the main function calculate_gann_values, which takes a single argument num. The variable y is initialized to the value of num, which will be used for comparison later in the code.
def calculate_gann_values(num):
y = num
Checker Function
Within the main function, we define an inner function called checker. This function checks if x is less than y and y is less than z. If this condition is met, it returns y; otherwise, it returns an empty string.
def checker(x, z):
if x < y < z:
return y
else:
return ""
Checking for Valid Input
Before performing calculations, we check if the input num is valid, ensuring it is not zero. In the context of the Gann Square of 9 Calculator, num represents a user-provided number, typically a significant price level.
if num:
Calculating Initial Values
In this section, we calculate several initial values based on the input num. We calculate the square root of num, subtract 2 from it, and round the result up to the nearest integer using math.ceil. The square of the rounded value is stored in the result variable.
root = num ** 0.5
minus_two = root - 2
rounded = math.ceil(minus_two)
result = rounded ** 2
Creating Lists
To store values calculated in the following steps, we create several empty lists: x, sqr_x, sqr_x_rounded, and sqr_x_rounded_root.
x = []
sqr_x = []
sqr_x_rounded = []
sqr_x_rounded_root = []
Generating Grid Values
We use a loop to generate values for x, sqr_x, sqr_x_rounded, and sqr_x_rounded_root. These values are based on the rounded value calculated earlier and specific increments. These values are essential for further calculations in the Gann Square of 9 grid.
for i in range(24):
x.append(rounded + 0.125 * (i + 1))
sqr_x.append(x[i] * x[i])
sqr_x_rounded.append(round(sqr_x[i] * 100) / 100)
sqr_x_rounded_root.append(round((num - sqr_x_rounded[i]) * 100) / 100)
Finding Support and Resistance Levels
In this part of the code, we identify the minimum positive index in the sqr_x_rounded_root list. This index is used to determine support and resistance levels in the Gann Square of 9 grid.
min_positive_index = -1
for i in range(len(sqr_x_rounded_root)):
if sqr_x_rounded_root[i] < 0:
min_positive_index = i
break
Initializing Lists for Levels
We initialize empty lists support, resistance, buy_target, and sell_target. These lists will store values representing support, resistance, buy target, and sell target levels.
support = []
resistance = []
buy_target = []
sell_target = []
Calculating Levels
This section calculates support, resistance, buy target, and sell target levels based on the minimum positive index. If a positive index is found, it calculates levels such as buy_above and sell_below, as well as support and resistance levels for five iterations. It also applies rounding to ensure precision in the target levels.
if min_positive_index >= 0:
buy_above = sqr_x_rounded[min_positive_index]
sell_below = sqr_x_rounded[min_positive_index - 1]
for i in range(5):
support.append(sqr_x_rounded[min_positive_index - 2 - i])
resistance.append(sqr_x_rounded[min_positive_index + 1 + i])
buy_target.append(roundup(resistance[i] * 0.9995, 2))
sell_target.append(roundup(support[i] * 1.0005, 2))
else:
buy_above = ""
sell_below = ""
support = [""] * 5
resistance = [""] * 5
buy_target = [""] * 5
sell_target = [""] * 5
Returning Results
Finally, the main function returns a dictionary containing calculated values. If the input num is not valid (zero or empty), it returns empty strings and lists for all values.
return {
"buy_above": buy_above,
"sell_below": sell_below,
"buy_target": buy_target,
"sell_target": sell_target
}
else:
return {
"buy_above": "",
"sell_below": "",
"buy_target": [""] * 5,
"sell_target": [""] * 5
}
Input and Calculation
In this section, the user provides an input value (in this case, number_input is set to 1409), and the calculate_gann_values function is called to compute Gann values. The calculated levels are stored in the result variable.
# Input from the user
number_input = 1409
# Calculate Gann values
result = calculate_gann_values(number_input)
The Complete Python Function That generates Gann Square of 9
import math
def calculate_gann_values(num):
y = num
def checker(x, z):
if x < y < z:
return y
else:
return ""
if num:
root = num ** 0.5
minus_two = root - 2
rounded = math.ceil(minus_two)
result = rounded ** 2
x = []
sqr_x = []
sqr_x_rounded = []
sqr_x_rounded_root = []
for i in range(24):
x.append(rounded + 0.125 * (i + 1))
sqr_x.append(x[i] * x[i])
sqr_x_rounded.append(round(sqr_x[i] * 100) / 100)
sqr_x_rounded_root.append(round((num - sqr_x_rounded[i]) * 100) / 100)
min_positive_index = -1
for i in range(len(sqr_x_rounded_root)):
if sqr_x_rounded_root[i] < 0:
min_positive_index = i
break
support = []
resistance = []
buy_target = []
sell_target = []
def roundup(number, places):
factor = 10 ** places
return round(number * factor) / factor
if min_positive_index >= 0:
buy_above = sqr_x_rounded[min_positive_index]
sell_below = sqr_x_rounded[min_positive_index - 1]
for i in range(5):
support.append(sqr_x_rounded[min_positive_index - 2 - i])
resistance.append(sqr_x_rounded[min_positive_index + 1 + i])
buy_target.append(roundup(resistance[i] * 0.9995, 2))
sell_target.append(roundup(support[i] * 1.0005, 2))
else:
buy_above = ""
sell_below = ""
support = [""] * 5
resistance = [""] * 5
buy_target = [""] * 5
sell_target = [""] * 5
return {
"buy_above": buy_above,
"sell_below": sell_below,
"buy_target": buy_target,
"sell_target": sell_target
}
else:
return {
"buy_above": "",
"sell_below": "",
"buy_target": [""] * 5,
"sell_target": [""] * 5
}
# Input from the user
number_input = 19845.76
# Calculate Gann values
result = calculate_gann_values(number_input)
result
The output comes as –
{'buy_above': 19845.77,
'sell_below': 19810.56,
'buy_target': [19871.06, 19906.31, 19941.58, 19976.9, 20012.24],
'sell_target': [19785.28, 19750.12, 19714.99, 19679.9, 19644.84]}
This basically gives us the trades to be followed as per the strategy for that day. Let’s beautify it slight more to get more perspective.
buy_above=result["buy_above"]
buy_target=result["buy_target"][0]
buy_sl=result["sell_below"]
sell_below=result["sell_below"]
sell_target=result["sell_target"][0]
sell_sl=result["buy_above"]
print("Buy Above:", buy_above)
print("Buy Target:", buy_target)
print("Buy Stop Loss:", buy_sl)
print("Sell Below:", sell_below)
print("Sell Target:", sell_target)
print("Sell Stop Loss:", sell_sl)
The output comes –
Buy Above: 1415.64
Buy Target: 1424.35
Buy Stop Loss: 1406.25
Sell Below: 1406.25
Sell Target: 1397.59
Sell Stop Loss: 1415.64
The output completely matches with the Gann Square of 9 Calcualator We have in Unofficed.
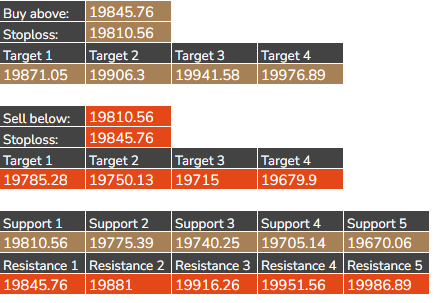

This Python script provides a comprehensive explanation of how to build a Python function for a Gann Square of 9 Calculator. It covers each part of the code and its role in calculating support, resistance, buy targets, and sell targets based on the Gann grid.

