Click here to download the Google Sheets
Click here to download the Excel Sheets

Inputs in Black-Scholes Option Pricing Model Formula

  • S0 = underlying price
  • X = strike price
  • σ = volatility
  • r = continuously compounded risk-free interest rate
  • q = continuously compounded dividend yield
  • t = time to expiration
For,
  • σ = Volatility = India VIX has been taken.
  • r = 10% (As per NSE Website, it is fixed.)
  • q = 0.00% (Assumed No Dividend)

 

Note: In many resources, you can find different symbols for some of these parameters in the Black Scholes Formula. For example,
  • The strike price is often denoted K (here it is X).
  • Underlying price is often denoted S (without the zero)
  • Time to expiration is often denoted T – t (difference between expiration and now).
In the original Black and Scholes paper (The Pricing of Options and Corporate Liabilities, 1973) the parameters were denoted x (underlying price), c (strike price), v (volatility), r (interest rate), and t* – t (time to expiration) in Black Scholes Formula. The dividend yield was only added by Merton in Theory of Rational Option Pricing, 1973.

Python Code

This python code patch is written for NSEPython Library first time. It will match with Zerodha’s Black Scholes Calculator perfectly.

				
					import math
from scipy.stats import norm

def black_scholes_dexter(S0,X,t,σ="",r=10,q=0.0,td=365):

  if(σ==""):σ =indiavix()

  S0,X,σ,r,q,t = float(S0),float(X),float(σ/100),float(r/100),float(q/100),float(t/td)
  #https://unofficed.com/black-scholes-model-options-calculator-google-sheet/

  d1 = (math.log(S0/X)+(r-q+0.5*σ**2)*t)/(σ*math.sqrt(t))
  #stackoverflow.com/questions/34258537/python-typeerror-unsupported-operand-types-for-float-and-int

  #stackoverflow.com/questions/809362/how-to-calculate-cumulative-normal-distribution
  Nd1 = (math.exp((-d1**2)/2))/math.sqrt(2*math.pi)
  d2 = d1-σ*math.sqrt(t)
  Nd2 = norm.cdf(d2)
  call_theta =(-((S0*σ*math.exp(-q*t))/(2*math.sqrt(t))*(1/(math.sqrt(2*math.pi)))*math.exp(-(d1*d1)/2))-(r*X*math.exp(-r*t)*norm.cdf(d2))+(q*math.exp(-q*t)*S0*norm.cdf(d1)))/td
  put_theta =(-((S0*σ*math.exp(-q*t))/(2*math.sqrt(t))*(1/(math.sqrt(2*math.pi)))*math.exp(-(d1*d1)/2))+(r*X*math.exp(-r*t)*norm.cdf(-d2))-(q*math.exp(-q*t)*S0*norm.cdf(-d1)))/td
  call_premium =math.exp(-q*t)*S0*norm.cdf(d1)-X*math.exp(-r*t)*norm.cdf(d1-σ*math.sqrt(t))
  put_premium =X*math.exp(-r*t)*norm.cdf(-d2)-math.exp(-q*t)*S0*norm.cdf(-d1)
  call_delta =math.exp(-q*t)*norm.cdf(d1)
  put_delta =math.exp(-q*t)*(norm.cdf(d1)-1)
  gamma =(math.exp(-r*t)/(S0*σ*math.sqrt(t)))*(1/(math.sqrt(2*math.pi)))*math.exp(-(d1*d1)/2)
  vega = ((1/100)*S0*math.exp(-r*t)*math.sqrt(t))*(1/(math.sqrt(2*math.pi))*math.exp(-(d1*d1)/2))
  call_rho =(1/100)*X*t*math.exp(-r*t)*norm.cdf(d2)
  put_rho =(-1/100)*X*t*math.exp(-r*t)*norm.cdf(-d2)

  return call_theta,put_theta,call_premium,put_premium,call_delta,put_delta,gamma,vega,call_rho,put_rho

Usage

				
					S0 = 34950.60
X = 35000.00
σ = 14.72
t = 3
call_theta,put_theta,call_premium,put_premium,call_delta,put_delta,gamma,vega,call_rho,put_rho=black_scholes_dexter(S0,X,t,σ="",r=10,q=0.0,td=365)
print(call_theta)
print(put_theta)
print(call_premium)
print(put_premium)
print(call_delta)
print(put_delta)
print(gamma)
print(vega)
print(call_rho)
print(put_rho)

Output

				
					-35.57594968706057
-25.994786756764814
175.92468507293597
196.56938065246504
0.4850057898780081
-0.514994210121992
0.0008543132102275919
12.621618527502404
1.378793315723619
-1.495555563365108

Call and Put Option Price Formulas

Call option C and put option P prices are calculated using the following formulas:

 

where N(x) is the standard normal cumulative distribution function.

The formulas for d1 and d2 are:

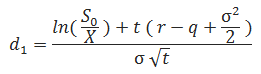
Original Black-Scholes vs. Merton’s Formulas

In the original Black-Scholes model, which doesn’t account for dividends, the equations are the same as above except:

  • There is just S0 in place of S0 e-qt
  • There is no q in the formula for d1

Therefore, if the dividend yield is zero, then e-qt = 1 and the models are identical.

Black-Scholes Formulas for Option Greeks

Delta

Theta

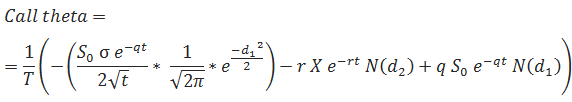
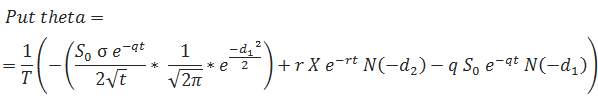
… where T is the number of days per year (calendar or trading days, depending on what you are using).

Gamma

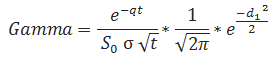
Vega

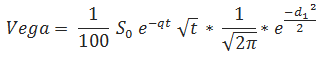
Rho

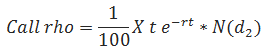
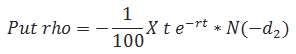
Join The Conversation?